GRAVITATIONAL WAVES: our scientists finally did it.....discovered a whole new room for new research and discoveries.......to explore.
In physics, gravitational waves are ripples in the curvature of space time which propagate as waves, travelling outward from the source. Predicted in 1916 by Albert Einstein on the basis of his theory of general relativity, gravitational waves transport energy as gravitational radiation.
The existence of gravitational waves is a possible consequence of the Lorentz invariance of general relativity since it brings the concept of a limiting speed of propagation of the physical interactions with it. By contrast, gravitational waves cannot exist in the Newtonian theory of gravitation, which postulates that physical interactions propagate at infinite speed.
Before the direct detection of gravitational waves, there was indirect evidence for their existence. For example, measurements of the Hulse–Taylor binary system suggest that gravitational waves are more than a hypothetical concept.
Potential sources of detectable gravitational waves include binary star systems composed of white dwarfs, neutron stars, and black holes. Various gravitational-wave detectors are under construction or in operation, such as Advanced LIGO which began observations in September 2015.
On 11th February 2016, the Advanced LIGO team announced that they had directly detected gravitational waves from a pair of black holes merging
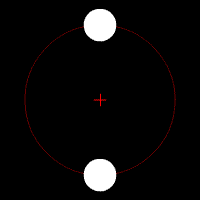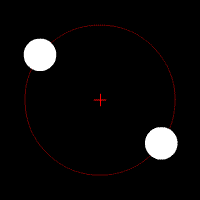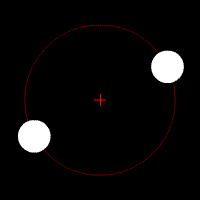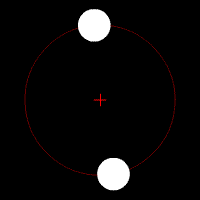
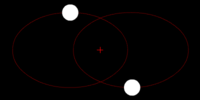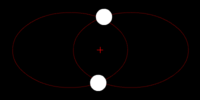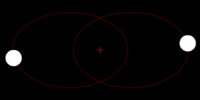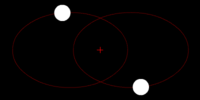
In general terms, gravitational waves are radiated by objects whose motion involves acceleration, provided that the motion is not perfectly spherically symmetric (like an expanding or contracting sphere) or cylindrical symmetric (like a spinning disk or sphere).
A simple example of this principle is a spinning dumbbell. If the dumbbell spins like a wheel on an axle, it will not radiate gravitational waves; if it tumbles end over end, as in the case of two planets orbiting each other, it will radiate gravitational waves.
The heavier the dumbbell, and the faster it tumbles, the greater is the gravitational radiation it will give off. In an extreme case, such as when the two weights of the dumbbell are massive stars like neutron stars or black holes, orbiting each other quickly, then significant amounts of gravitational radiation would be given off.
A schematic diagram of a laser interferometer
Some more detailed examples:
- Two objects orbiting each other in a quasi-Keplerian planar orbit (basically, as a planet would orbit the Sun) will radiate.
- A spinning non-axisymmetric planetoid — say with a large bump or dimple on the equator — will radiate.
- A supernova will radiate except in the unlikely event that the explosion is perfectly symmetric.
- An isolated non-spinning solid object moving at a constant velocity will not radiate. This can be regarded as a consequence of the principle of conservation of linear momentum.
- A spinning disk will not radiate. This can be regarded as a consequence of the principle of conservation of angular momentum. However, it will show gravitomagnetic effects.
- A spherically pulsating spherical star (non-zero monopole moment or mass, but zero quadrupole moment) will not radiate, in agreement with Birkhoff's theorem.
More technically, the third time derivative of the quadrupole moment of an isolated system's stress–energy tensor must be nonzero in order for it to emit gravitational radiation.
This is analogous to the changing dipole moment of charge or current necessary for electromagnetic radiation
Power radiated by orbiting bodies
Gravitational waves carry energy away from their sources and, in the case of orbiting bodies, this is associated with an inspiral or decrease in orbit.
Imagine for example a simple system of two masses — such as the Earth-Sun system — moving slowly compared to the speed of light in circular orbits.
Assume that these two masses orbit each other in a circular orbit in the x–y plane. To a good approximation, the masses follow simple Keplerian orbits.
However, such an orbit represents a changing quadrupole moment. That is, the system will give off gravitational waves.
Suppose that the two masses are  and
and 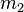 , and they are separated by a distance
, and they are separated by a distance  . The power given off (radiated) by this system is:
. The power given off (radiated) by this system is:
 and
and 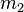 , and they are separated by a distance
, and they are separated by a distance  . The power given off (radiated) by this system is:
. The power given off (radiated) by this system is:
where G is the gravitational constant, c is the speed of light in vacuum and where the negative sign means that power is being given off by the system, rather than received.
For a system like the Sun and Earth,  is about 1.5×1011 m and
is about 1.5×1011 m and  and
and 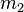 are about 2×1030 and 6×1024 kg respectively. In this case, the power is about 200 watts.
are about 2×1030 and 6×1024 kg respectively. In this case, the power is about 200 watts.
 is about 1.5×1011 m and
is about 1.5×1011 m and  and
and 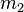 are about 2×1030 and 6×1024 kg respectively. In this case, the power is about 200 watts.
are about 2×1030 and 6×1024 kg respectively. In this case, the power is about 200 watts.
This is truly tiny compared to the total electromagnetic radiation given off by the Sun (roughly 3.86×1026 watts).
In theory, the loss of energy through gravitational radiation could eventually drop the Earth into the Sun. However, the total energy of the Earth orbiting the Sun (kinetic energy +gravitational potential energy) is about 1.14×1036 joules of which only 200 joules per second is lost through gravitational radiation, leading to a decay in the orbit by about 1×10−15 meters per day or roughly the diameter of a proton.
At this rate, it would take the Earth approximately 1×1013 times more than the current age of the Universe to spiral onto the Sun.
This estimate overlooks the decrease in r over time, but the majority of the time the bodies are far apart and only radiating slowly, so the difference is unimportant in this example.
A more dramatic example of radiated gravitational energy is represented by two solar mass (M☉) neutron stars orbiting at a distance from each other of 1.89×108 m (only 0.63 light-seconds apart). [The Sun is 8 light minutes from the Earth.] Plugging their masses into the above equation shows that the gravitational radiation from them would be 1.38×1028 watts, which is about 100 times more than the Sun's electromagnetic radiation.
for details go to:
- Gravitational wave background
- Gravitational field
- Gravitomagnetism
- Graviton
- Gravitational wave astronomy
- Hawking radiation, for gravitationally induced electromagnetic radiation from black holes
- HM Cancri
- LIGO, Virgo interferometer, GEO600, KAGRA, and TAMA 300 — Ground-based gravitational-wave detectors
- Linearised Einstein field equations
- LISA, DECIGO and BBO — Proposed space-based detectors
- Peres metric
- pp-wave spacetime, for an important class of exact solutions modelling gravitational radiation
- PSR B1913+16, the first binary pulsar to be discovered and the first experimental evidence for the existence of gravitational waves.
- Spin-flip, a consequence of gravitational wave emission from binary supermassive black holes
- Sticky bead argument, for a physical way to see that gravitational radiation should carry energy
- Tidal force
THANK YOU FOR VISITING...........STAY EXPLORING.....



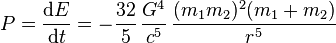
No comments:
Post a Comment